Chapter 2 Causal Graphs
2.1 The Fork
We first simulate some data from the simple ‘Fork’ DAG.
set.seed(1747)
n <- 1e4
bZ <- 1
Z <- rnorm(n, 0, 1)
X <- Z*bZ + rnorm(n, 0, 1)
Y <- Z*bZ + rnorm(n, 0, 1)We then write a function for fitting and plotting our models that we can re-use for the ‘Pipe’ and ‘Collider’ scenarios. This function depends on the ggplot2 (H. Wickham et al. 2019) and patchwork (Pedersen 2024) packages.
library(ggplot2)
library(patchwork)
plot_scat <- function(data, title){
# Y ~ X
p1 <- ggplot(data, aes(x=X, y=Y)) +
geom_point(alpha = 0.05, size = .1) +
geom_smooth(method='lm', color = "blue", linewidth = 0.5) +
theme_classic() +
labs(title = title, subtitle = "Y ~ X")
# Y ~ X + Z
model <- lm(Y ~ X + Z, data = data)
new_data <- transform(data,
Z = 0)
predictions <- predict(model, newdata = new_data, interval = "confidence")
p2 <- ggplot(data, aes(x = X, y = Y)) +
geom_point(alpha = 0.05, size = .1) +
geom_line(data = new_data, aes(y = predictions[, "fit"]), linewidth = 0.5, color = "blue") +
geom_ribbon(data = new_data, aes(ymin = predictions[, "lwr"], ymax = predictions[, "upr"]), alpha = 0.2) +
theme_classic() +
labs(subtitle = "Y ~ X + Z")
return(p1 + p2)
}We then apply the function to the simulated data.
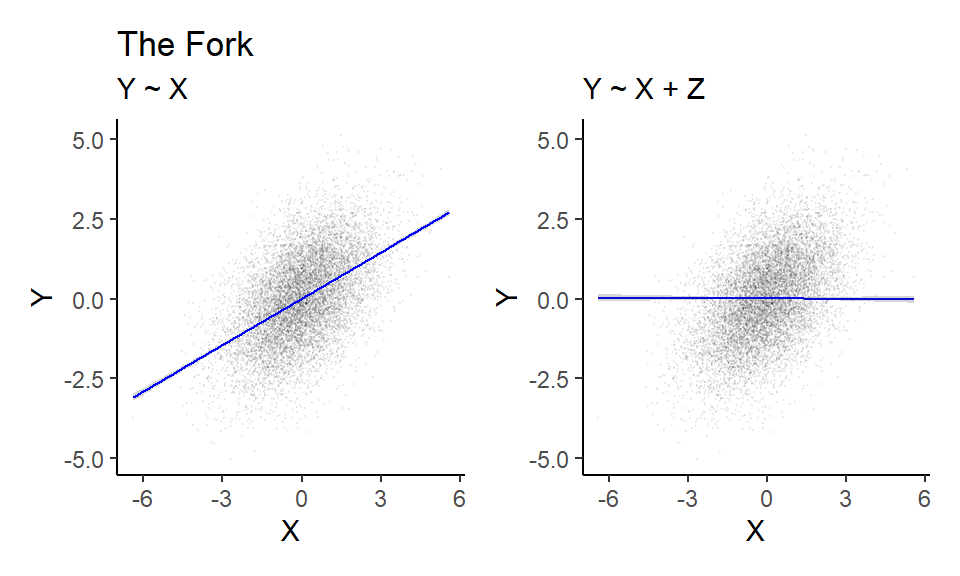
2.2 The Pipe
Similarly to above, we simulate data from the ‘Pipe’ DAG…
set.seed(1747)
n <- 1e4
bZ <- 1
bX <- 1
X <- rnorm(n, 0, 1)
Z <- X*bX + rnorm(n, 0, 1)
Y <- Z*bZ + rnorm(n, 0, 1)… and then apply our custom fitting and plotting function.
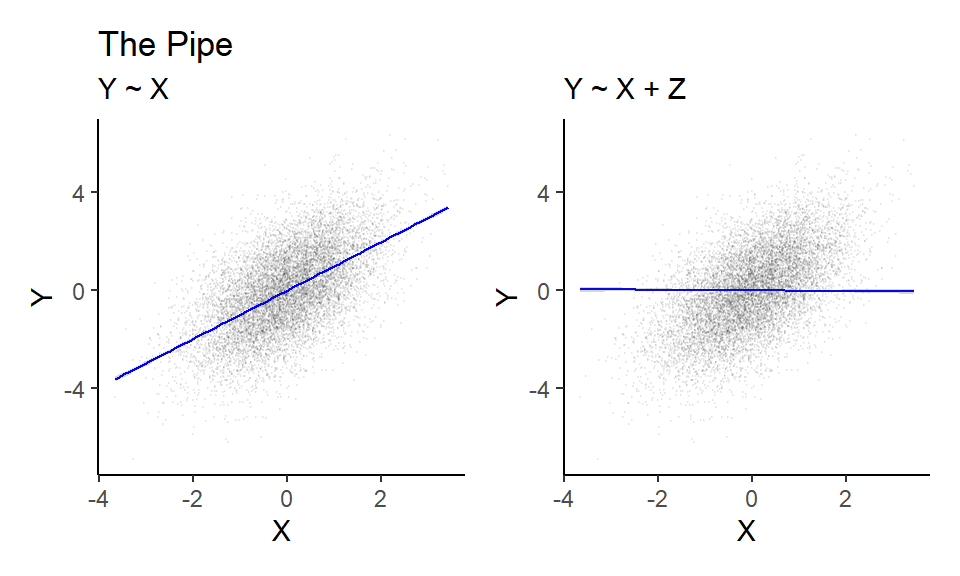
2.3 The Collider
Exactly the same approach as above.
set.seed(1747)
n <- 1e4
bX <- 1
bY <- 1
X <- rnorm(n, 0, 1)
Y <- rnorm(n, 0, 1)
Z <- X*bX + Y*bY + rnorm(n, 0, 1)
plot_scat(data = data.frame(Y=Y, X=X, Z=Z), title = "The Collider")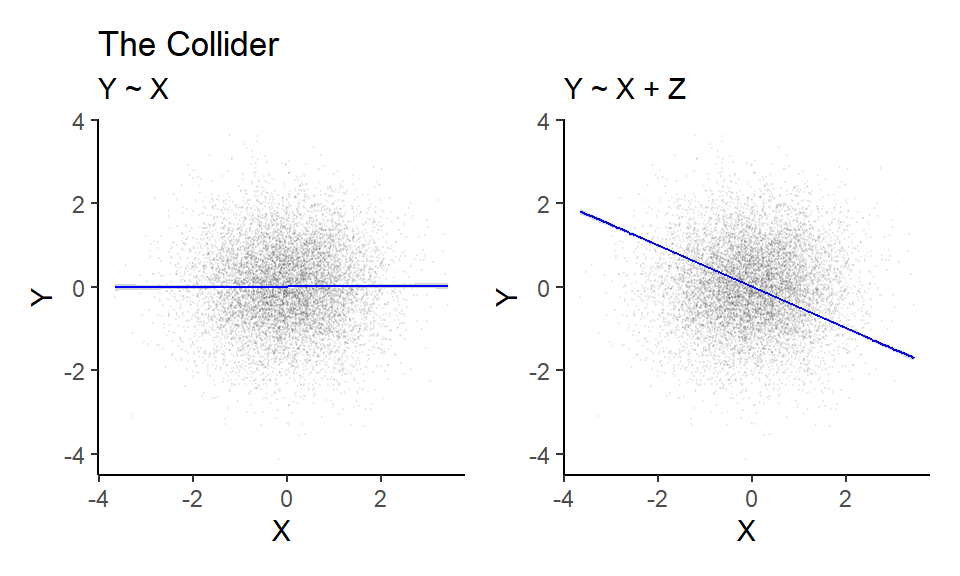
2.4 Post-treatment bias
Again, following the same approach, we simulate data from the post-treatment DAG.
set.seed(1747)
n <- 1e4
bZ <- 1
bX <- 0.5
bY <- 1
Z <- rnorm(n, 0, 1)
X <- Z*bZ + rnorm(n, 0, 1)
Y <- Z*bZ + X*bX + rnorm(n, 0, 1)
P <- Y*bY + rnorm(n, 0, 1)Next, we fit two models: One that adjusts for the post-treatment variable P…
##
## Call: glm(formula = Y ~ X + Z + P, data = data.frame(Y = Y, X = X,
## Z = Z, P = P))
##
## Coefficients:
## (Intercept) X Z P
## 0.01018 0.25354 0.50133 0.48813
##
## Degrees of Freedom: 9999 Total (i.e. Null); 9996 Residual
## Null Deviance: 34040
## Residual Deviance: 4895 AIC: 21240… and another that doesn’t.
##
## Call: glm(formula = Y ~ X + Z, data = data.frame(Y = Y, X = X, Z = Z))
##
## Coefficients:
## (Intercept) X Z
## 0.007601 0.495594 0.987202
##
## Degrees of Freedom: 9999 Total (i.e. Null); 9997 Residual
## Null Deviance: 34040
## Residual Deviance: 9793 AIC: 28180We see that only the latter model picks up the correct estimate for X, which was 0.5 in this case.
2.5 Session info
## R version 4.4.1 (2024-06-14 ucrt)
## Platform: x86_64-w64-mingw32/x64
## Running under: Windows 10 x64 (build 19045)
##
## Matrix products: default
##
##
## locale:
## [1] LC_COLLATE=Danish_Denmark.utf8 LC_CTYPE=Danish_Denmark.utf8
## [3] LC_MONETARY=Danish_Denmark.utf8 LC_NUMERIC=C
## [5] LC_TIME=Danish_Denmark.utf8
##
## time zone: Europe/Copenhagen
## tzcode source: internal
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] patchwork_1.3.0 ggplot2_3.5.1
##
## loaded via a namespace (and not attached):
## [1] Matrix_1.7-0 gtable_0.3.5 jsonlite_1.8.8 highr_0.11
## [5] dplyr_1.1.4 compiler_4.4.1 tidyselect_1.2.1 jquerylib_0.1.4
## [9] splines_4.4.1 scales_1.3.0 yaml_2.3.8 fastmap_1.2.0
## [13] lattice_0.22-6 R6_2.5.1 labeling_0.4.3 generics_0.1.3
## [17] knitr_1.47 tibble_3.2.1 bookdown_0.41 munsell_0.5.1
## [21] bslib_0.7.0 pillar_1.9.0 rlang_1.1.4 utf8_1.2.4
## [25] cachem_1.1.0 xfun_0.48 sass_0.4.9 cli_3.6.2
## [29] withr_3.0.0 magrittr_2.0.3 mgcv_1.9-1 digest_0.6.35
## [33] grid_4.4.1 rstudioapi_0.16.0 lifecycle_1.0.4 nlme_3.1-164
## [37] vctrs_0.6.5 evaluate_0.24.0 glue_1.7.0 farver_2.1.2
## [41] fansi_1.0.6 colorspace_2.1-0 rmarkdown_2.27 tools_4.4.1
## [45] pkgconfig_2.0.3 htmltools_0.5.8.1References
Pedersen, Thomas Lin. 2024. patchwork: The Composer of Plots. https://CRAN.R-project.org/package=patchwork.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the tidyverse.” Journal of Open Source Software 4 (43): 1686. https://doi.org/10.21105/joss.01686.